
Using some non-trivial math computations from the number theory, find three very large integers e, d and n, such that:

Generating an RSA public + private key pair involves the following: key generation may take from several minutes to several hours. 50000 bits or 65536 bits) may be too slow for practical use, e.g. Longer keys provide higher security but consume more computing time, so there is a tradeoff between security and speed.
Key length of 3072-bits and above are considered secure. RSA can work with keys of different keys of length: 1024, 2048, 3072, 4096, 8129, 16384 or even more bits.
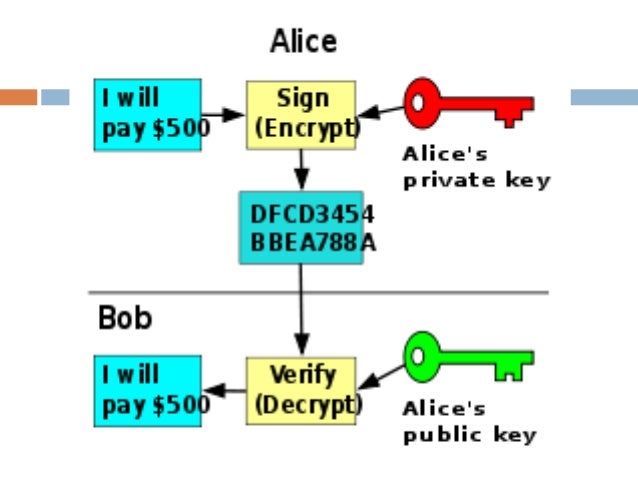
Key exchange: securely transport a secret key, used for encrypted communication later. Digital signatures: sign messages (using the private key) and verify message signature (using the public key). Encryption: encrypt a secret message (integer in the range ) using the public key and decrypt it back using the secret key. Key-pair generation: generate random private key (typically of size 1024-4096 bits) and corresponding public key. Later, when ECC cryptography evolved, the ECC slowly became dominant in the asymmetric cryptosystems, because of its higher security and shorter key lengths than RSA. The RSA algorithm is named after the initial letters of its authors ( Rivest– Shamir– Adleman) and is widely used in the early ages of computer cryptography. The RSA cryptosystem is one of the first public-key cryptosystems, based on the math of the modular exponentiations and the computational difficulty of the RSA problem and the closely related integer factorization problem ( IFP).







 0 kommentar(er)
0 kommentar(er)
